I've been reading and thinking a lot about cognitive load theory in Geometry class, thanks to Michael Pershan, Greg Ashman, Dylan Wiliam, and Ilana Horn.
I've pared back what I ask students to do using a new structure I've been calling "Ten True Statements." It could be twelve or eight or nine, but ten is a nice number. Here's the basic idea.
Students are given a problem that includes a diagram and a statement, but my instructions to them are extremely non-pathway-specific. I ask them to generate at least ten true statements about the situation. I given them a specific amount of time and then I yell, "GO!"
I circulate, but only provide just-enough of a hint to table groups to help them get themselves unstuck. The purpose here is to learn how to ask for help and not just stay stuck.
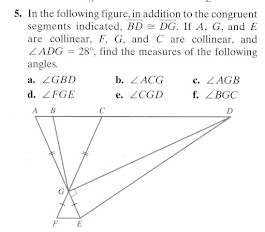
Here's one of the problems they did on Thursday:
I consider this activity purely generative. Students need practice in brainstorming.
I want them to lose themselves in flow so they can practice using their reference materials to develop as many ideas (aka "true statements") about the figure as they can, together with justification.
I don't care about the order of statements. I don't care if statements are relevant to a proof pathway.
The habits of mind I am trying to cultivate are to learn how to brainstorm more gently with their minds without judgment; to use their tools as a memory aid; and to document their thinking process.
My theory of action is this: the more practice they have in generating true statements and in deriving new true statements from previous true statements they have generated, the easier it will be for them to learn how to put their true statements and justifications into order.
I am trying to focus their working memory just on the generation of true statements.
All four classes are really loving this activity, so I have to go find more suitable problems for the week.
Love this idea. What are some of the things they said were true for this example?
ReplyDeleteTHAT was incredibly revealing for each table group and gave me a ton of formative assessment data on where they were at in their understanding. Some groups started by restating the given information as discrete true statements, such as "BD=DG." Less confident groups often said things like "Triangle BDG is isosceles." That gave me the opening I needed to help them connect their reference materials to what they could identify on the diagram.
DeleteMore fluent/confident groups of learners dove into annotating their diagrams with color and other indicators. In general, the more annotations on their diagram, the more mature their understanding was. The groups that had accumulated more statements started spontaneously drawing arrows between and among statements. That told me a lot about their understanding of implication and sequencing.
This gave me a lot of flexibility to coach the groups who felt really lost, asking them which things in the diagram they could confidently annotate, asking them to state the names of things, etc.
I got an enormous amount of information on where students are, and how variable it is from one course section to another.
This comment has been removed by a blog administrator.
ReplyDeleteI really like this activity. It gets me thinking of how I can use it. Since I do a lot of stations/rotations, I could see putting one up on the board and having the first small group list statements. Then the second group can: a) put a check box after a statement they agree with; b) put a question mark after a statement they believe is incorrect; c) add new statements. I'm curious how this has evolved since you posted last year. I'm new to the blog and find it fascinating.
ReplyDeleteEncourages Depth of Understanding: By asking students to generate multiple true statements, you push them to think deeply about the problem. It challenges them to recognize patterns and relationships that may not be immediately obvious.
ReplyDeleteCentralized Dust Collector india
Paint booth India
Reduces Cognitive Overload: The structure of asking for "true statements" rather than focusing on solving the problem in a specific way helps avoid overwhelming students with complex, step-by-step solutions. It allows them to approach the problem from various angles without being burdened by a rigid pathway.
ReplyDeleteShrink Packing machine India
Shrink wrapping machine India
Promotes Autonomy: The fact that you allow students to work independently, yet provide just enough of a hint when they get stuck, encourages them to take ownership of their learning. It’s a great way to foster problem-solving skills and resilience.
ReplyDeleteCartridge type bag filter manufacturer delhi
Induced Draft Fan in Delhi
Fosters Collaboration: Since you're encouraging students to work in table groups, this approach also promotes peer collaboration. Students can share their insights and build upon each other’s ideas, making the learning experience more social and dynamic.
ReplyDeleteCartridge type bag filter India
Axial Flow Fans India
Metacognitive Skills: Asking students to reflect on what makes a statement true or false will help them develop their metacognitive abilities. They have to be aware of their own thought processes and strategies, which is crucial for long-term learning.
ReplyDeleteInvest in Brands
Dust Cleaner
Flexibility in Problem-Solving: The open-ended nature of the task means that students are free to explore different aspects of the geometry problem. This flexibility can lead to more creative solutions and a better understanding of the topic.
ReplyDeletePollution Control Equipments
Centrifugal Blowers
Promotes Help-Seeking Behaviors: Your emphasis on students asking for help when they're stuck is valuable. It shifts the focus from a "right or wrong" mindset to a more growth-oriented one, where students learn that seeking assistance is an integral part of the learning process.
ReplyDeleteEvaporative aircooling system manufacturer
Dust Cleaner india